正方形对角线

欢迎关注“陈老师初中数理化”，一起探索快乐学习的奥秘！

在初二数学中，利用正方形性质求解动点轨迹是一类典型问题。本文将结合例题，深入浅出地解析这类问题的解题思路，帮助同学们提升数学解题能力。

问题描述：如图所示，在平面直角坐标系中，边长为a（a是大于0的常数的正方形ABCD的对角线AC、BD相交于点P。顶点A在x轴正半轴上运动，顶点B在y轴正半轴上运动（x轴正半轴和y轴正半轴均不包含原点O，顶点C、D位于第一象限。

（1当∠BAO=45°时，求点P的坐标；

（2证明：无论点A在x轴正半轴上、点B在y轴正半轴上如何运动，点P始终位于∠AOB的平分线上。

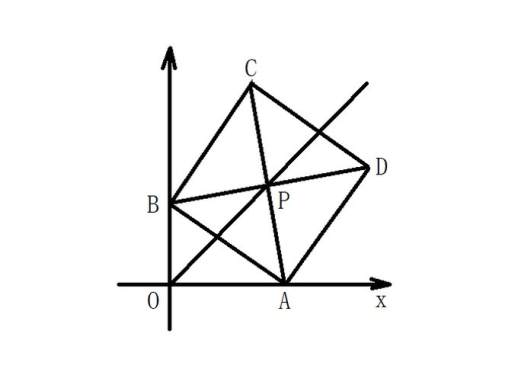
解题步骤：

1. 当∠BAO=45°时，求点P的坐标

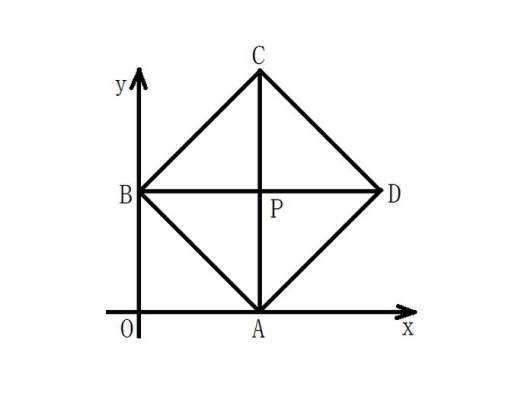
根据正方形的性质和题设条件：四边形ABCD是正方形，可知AC平分∠BAD，∠BAD=90°，AC⊥BD，AP=BP。

由于AC平分∠BAD且∠BAD=90°，可得∠BAC=∠BAD/2=45°。

结合题设条件和推论：∠BAO=45°，∠BAC=45°，可得∠OAP=∠BAC+∠BAO=90°，即AC⊥x轴。

根据平行线的判定和推论：AC⊥BD，AC⊥x轴，可得BD∥x轴。

根据平行线的性质和推论：BD∥x轴，∠AOB=90°，可得∠DBO+∠AOB=180°，即∠DBO=90°，BP⊥y轴。

根据勾股定理和推论：AB=a，BP=AP，AB^2=AP^2+BP^2，可得AP=BP=√2/2a。

综上所述：AP=BP=√2/2a，BP⊥y轴，AC⊥x轴，因此点P的坐标为(√2/2a, √2/2a)。

2. 证明：点P始终位于∠AOB的平分线上

过点P作PE⊥x轴，PF⊥y轴，如下图所示：

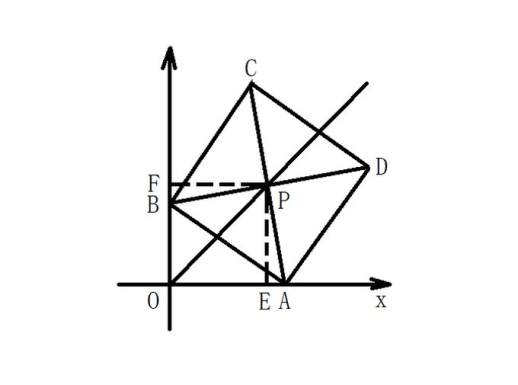
根据题设条件：PE⊥x轴，PF⊥y轴，AC⊥BD，可得∠PEA=∠PFB=∠PEO=∠APB=90°。

由于∠PFB=∠PEO=90°，∠AOB=90°，可得∠FPE=90°。

由于∠FPE=∠APB=90°，∠FPE=∠BPE+∠BPF，∠APB=∠BPE+∠APE，可得∠BPF=∠APE。

根据全等三角形的判定和推论：∠BPF=∠APE，∠PFB=∠PEA，BP=AP，可得△BFP≌△AEP。

根据全等三角形的性质和推论：△BFP≌△AEP，可得PE=PF。

根据角平分线的判定和推论：PE⊥x轴，PF⊥y轴，PE=PF，可知点P位于∠AOB的平分线上。

解题的关键在于利用正方形的性质推导出线段和角度之间的数量关系，通过构造全等三角形得到线段之间的等量关系，从而证明题目所需的结论。

根据题目中的条件：线段PE垂直于x轴，线段PF垂直于y轴，线段AC垂直于线段BD，于是∠PEA=∠PFB=∠PEO=∠APB=90°。
根据题目的结论：∠PFB=∠PEO=90°，∠AOB=90°，因此可推出∠FPE=90°。
根据题目的结论：∠FPE=∠APB=90°，∠FPE=∠BPE+∠BPF，∠APB=∠BPE+∠APE，由此可得到∠BPF=∠APE。
凭借全等三角形的判定与题目的结论：∠BPF=∠APE，∠PFB=∠PEA，BP=AP，从而可推出△BFP≌△AEP。
根据全等三角形的性质与题目的结论：△BFP≌△AEP，于是可得到PE=PF。
根据角平分线的判定与题目的结论：线段PE垂直于x轴，线段PF垂直于y轴，PE=PF，故点P位于∠AOB的平分线上。
解决此题的关键在于综合运用正方形的性质，由此得出线段与角度之间的数量关系，进而通过构造全等三角形得出线段等量的关系，最后证明题目指向的结论。